Last updated: 2020-12-20

Checks: 7 0

Knit directory: gacha/

This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20201216)

The command set.seed(20201216) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: abbc19b

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version abbc19b. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 


Ignored files:
    Ignored:    .DS_Store
    Ignored:    .RData
    Ignored:    .Rhistory
    Ignored:    gacha/.RData
    Ignored:    gacha/.Rhistory

Untracked files:
    Untracked:  analysis/compare.Rmd
    Untracked:  analysis/shiny.Rmd

Unstaged changes:
    Modified:   code/wflow_init.R

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/gacha.Rmd) and HTML (docs/gacha.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File Version Author Date Message
html b206e5c Lijia Wang 2020-12-20 Build site.
html 8fbcdf9 Lijia Wang 2020-12-18 Build site.
html 9f25d18 Lijia Wang 2020-12-18 Build site.
html 3e046d1 Lijia Wang 2020-12-17 Build site.
Rmd 985204e Lijia Wang 2020-12-17 appended 10-pull bonus
html 2357df5 Lijia Wang 2020-12-17 Build site.
html e97114c Lijia Wang 2020-12-17 Build site.
Rmd 81db14e Lijia Wang 2020-12-17 10-pull bonus (WIP)
html 1ba59f6 Lijia Wang 2020-12-16 Build site.
html 998f5f3 Lijia Wang 2020-12-16 Build site.
Rmd e77d1c4 Lijia Wang 2020-12-16 single pulls

Introduction

In this section, we will introduce and model a gacha scenario where all characters in the same rarity level have the same probability of getting pulled, and pulls are performed one at a time (therefore no bonuses are applied). We would like to find the expected number of trials until we obtain any SSR character.

Method

Pulls can be modeled as a Bernoulli Process

In this scenario, the probability of getting each tier is constant, and the probability to pull each character within the tier is the same. Let the probability of pulling an SSR be \(p\), and suppose there are \(n\) characters in the SSR tier, then the probability to pull each individual SSR character is \(\frac{p}{n}\). We also assume that pulls are performed one at a time and under the assumption that no previous pull affects the result of the next pull.

This process can be modeled as a simple Bernoulli process with an unfair coin, where probability of obtaining an SSR character (“success”) is \(p\) and not obtaining an SSR (“failure”) is \((1-p)\). This means we would probably expect on average \(1/p\) pulls to obtain the first SSR.

Poisson Distribution

We notice that the probability of success \(p\) is typically very small in each gacha game, ranging from 0.600% (Genshin Impact) to 2.000% (Arknights) in the examples we use. Therefore, we are safe to approximate the probability of SSR pulls with a Poisson distribution.

\[ f(k; \lambda) = Pr(X=k) = \frac{\lambda^k}{k!}e^{-\lambda} \]

Since \(p\) small, we can approximate \(\lambda = np\). We can subsequently rephrase our question into “in how many trials can we maximize the probability of obtaining exactly 1 SSR card”?

Application in F/GO

We plotted the probabilities of obtaining 1, 2, and 3 SSR cards in 1 to 500 pulls. Here we used the Fate/Grand Order Saint Quartz Summon Distribution Rate on an non-event banner. We define “success” as pulling a 5-star servant (character), and the probability is 1.000% (according to in-game statistics provided).

[1] "Number of pulls that maximizes probability of 1 SSR is 100"
[1] "Number of pulls that maximizes probability of 2 SSRs is 200"
[1] "Number of pulls that maximizes probability of 3 SSRs is 300"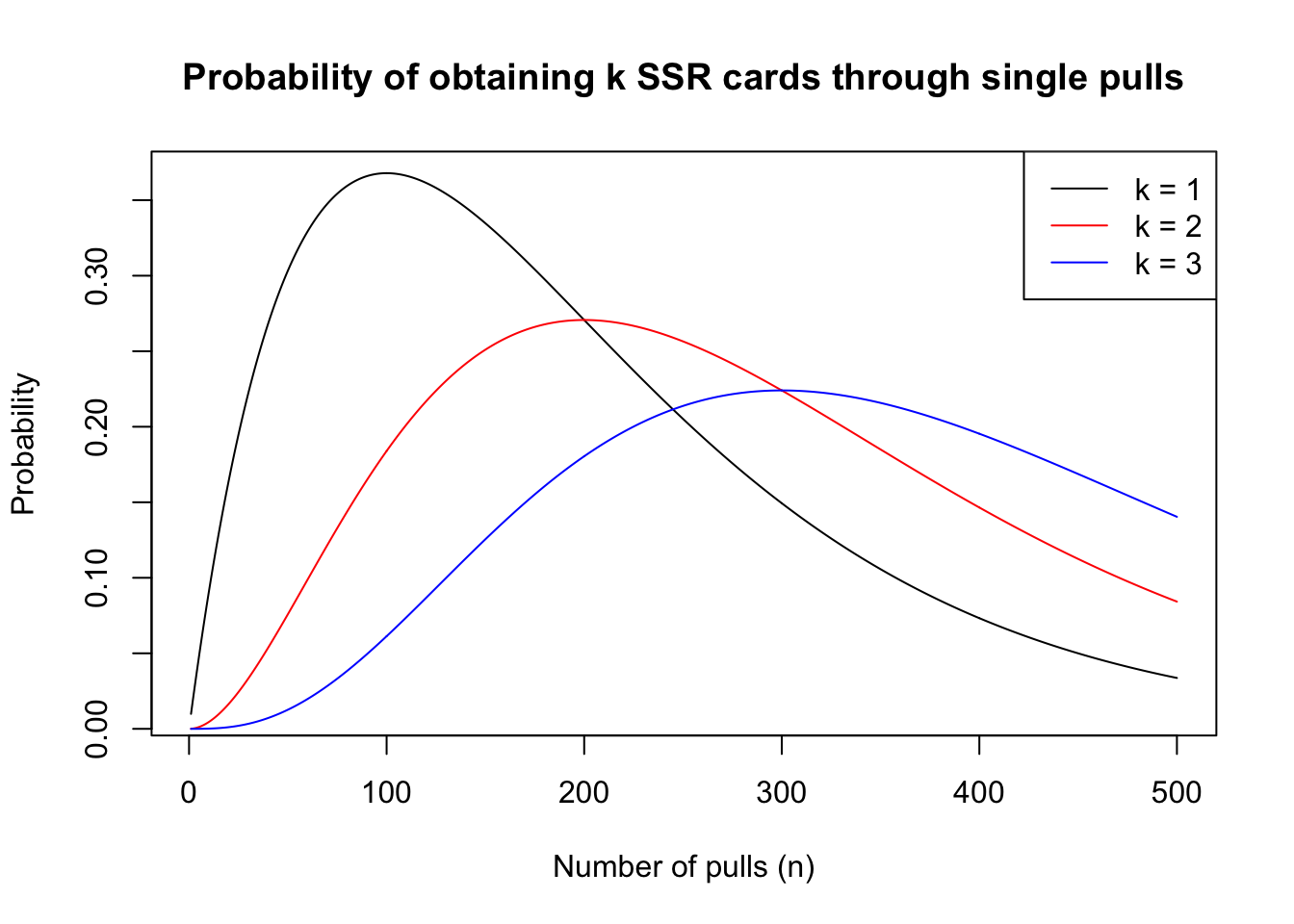

Version Author Date
998f5f3 Lijia Wang 2020-12-16

Trials to first Success

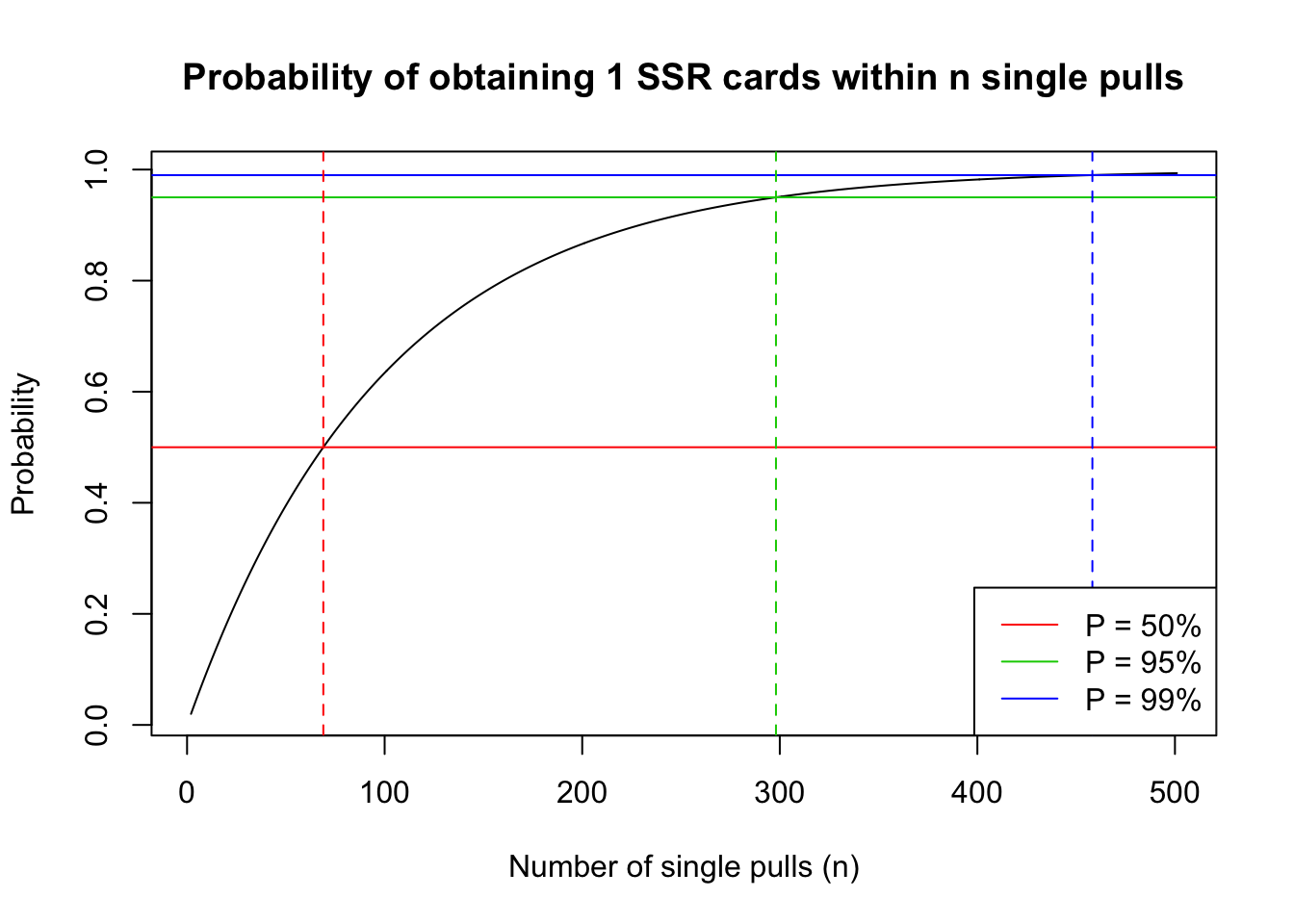
We know that our probability of pulling 1 character is maximized at 100 single pulls, but that information itself is not all that useful. We will use the cumulative distribution function to explore at what point we will obtain a 95% chance of pulling an SSR character through single pulls only.

Each pull is a Bernoulli Variable \(X_i\) and are independentally and identically distributed. Therefore, we can apply the geometric distribution and obtain the probability of obtaining the first success at the \(k\)-th trial:

\[ Pr(X=k) = (1-p)^{k-1}p\]

and we have the cumulative distribution function:

\[ Pr(X\leq k) = 1-(1-p)^k \]

And we would like to find the number \(k\) when \(Pr(X\leq k) \geq 0.95\), which can be easily computed given probability \(p\).

Application in F/GO

In the F/GO case, If we would like to achieve 50% chance of getting an SSR:

\[ Pr(X\leq k) = 1-(1-p)^k = 1-(1-0.01)^k = 0.50\]

\[ k = \frac{log(0.50)}{log(1-0.01)} = 68.96\]

If we would like to achieve 95% chance of getting an SSR:

\[ Pr(X\leq k) = 1-(1-p)^k = 1-(1-0.01)^k = 0.95\]

\[ k = \frac{log(0.05)}{log(1-0.001)} = 298.07\]

And for 99% chance, you would get:

\[ k = \frac{log(0.01)}{log(1-0.01)} = 458.21\]

This means if you saved up for 459 single pulls, you are almost guaranteed to obtain an SSR character from the gacha.

Visualization

Version Author Date
3e046d1 Lijia Wang 2020-12-17 

R version 3.6.2 (2019-12-12)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS  10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] workflowr_1.6.2

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.3      rprojroot_1.3-2 digest_0.6.25   later_1.0.0    
 [5] R6_2.4.1        backports_1.1.5 git2r_0.26.1    magrittr_1.5   
 [9] evaluate_0.14   stringi_1.4.6   rlang_0.4.5     fs_1.3.2       
[13] promises_1.1.0  whisker_0.4     rmarkdown_2.1   tools_3.6.2    
[17] stringr_1.4.0   glue_1.3.2      httpuv_1.5.2    xfun_0.12      
[21] yaml_2.2.1      compiler_3.6.2  htmltools_0.4.0 knitr_1.28